Home  ›  Forward Difference Error Function Only Continuous

Forward Difference Error Function Only Continuous

Written By Sunday, 16 October 2022 Add Comment Edit

Interpolation is the technique of estimating the value of a function for any intermediate value of the independent variable, while the process of computing the value of the function outside the given range is called extrapolation.

Forward Differences: The differences y1 – y0, y2 – y1, y3 – y2, ……, yn – yn–1 when denoted by dy0, dy1, dy2, ……, dyn–1 are respectively, called the first forward differences. Thus, the first forward differences are :
\Delta Y_{r}=Y_{r+1}-Y_{r}

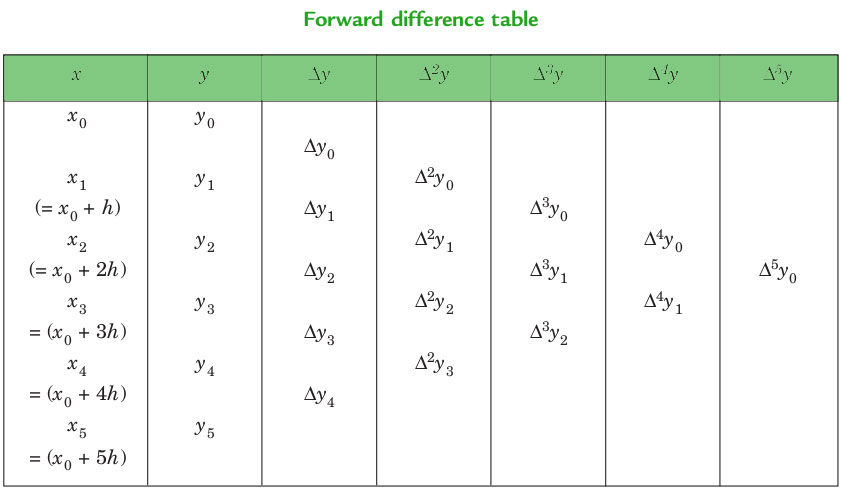
NEWTON'S GREGORY FORWARD INTERPOLATION FORMULA :
f(a+hu)=f(a)+u\Delta f(a)+\frac{u\left ( u-1 \right )}{2!}\Delta ^{2}f(a)+...+\frac{u\left ( u-1 \right )\left ( u-2 \right )...\left ( u-n+1 \right )}{n!}\Delta ^{n}f(a)
This formula is particularly useful for interpolating the values of f(x) near the beginning of the set of values given. h is called the interval of difference and u = ( x – a ) / h, Here a is the first term.

Example :

Input : Value of Sin 52

Output :

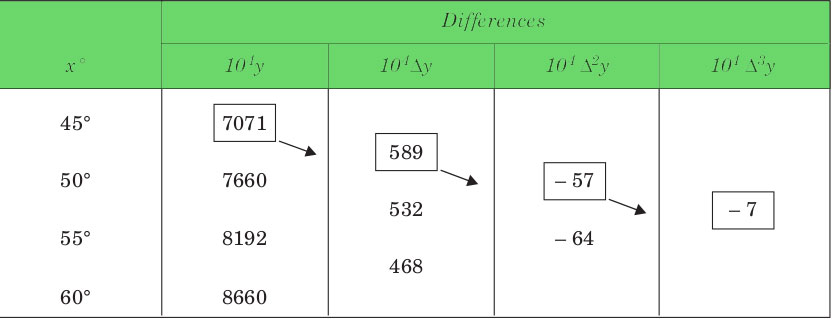
          Value at Sin 52 is 0.788003

Below is the implementation of the Newton forward interpolation method.

C++

#include <bits/stdc++.h>

using namespace std;

float u_cal( float u, int n)

{

float temp = u;

for ( int i = 1; i < n; i++)

temp = temp * (u - i);

return temp;

}

int fact( int n)

{

int f = 1;

for ( int i = 2; i <= n; i++)

f *= i;

return f;

}

int main()

{

int n = 4;

float x[] = { 45, 50, 55, 60 };

float y[n][n];

y[0][0] = 0.7071;

y[1][0] = 0.7660;

y[2][0] = 0.8192;

y[3][0] = 0.8660;

for ( int i = 1; i < n; i++) {

for ( int j = 0; j < n - i; j++)

y[j][i] = y[j + 1][i - 1] - y[j][i - 1];

}

for ( int i = 0; i < n; i++) {

cout << setw(4) << x[i]

<< "\t" ;

for ( int j = 0; j < n - i; j++)

cout << setw(4) << y[i][j]

<< "\t" ;

cout << endl;

}

float value = 52;

float sum = y[0][0];

float u = (value - x[0]) / (x[1] - x[0]);

for ( int i = 1; i < n; i++) {

sum = sum + (u_cal(u, i) * y[0][i]) /

fact(i);

}

cout << "\n Value at " << value << " is "

<< sum << endl;

return 0;

}

Java

class GFG{

static double u_cal( double u, int n)

{

double temp = u;

for ( int i = 1 ; i < n; i++)

temp = temp * (u - i);

return temp;

}

static int fact( int n)

{

int f = 1 ;

for ( int i = 2 ; i <= n; i++)

f *= i;

return f;

}

public static void main(String[] args)

{

int n = 4 ;

double x[] = { 45 , 50 , 55 , 60 };

double y[][]= new double [n][n];

y[ 0 ][ 0 ] = 0.7071 ;

y[ 1 ][ 0 ] = 0.7660 ;

y[ 2 ][ 0 ] = 0.8192 ;

y[ 3 ][ 0 ] = 0.8660 ;

for ( int i = 1 ; i < n; i++) {

for ( int j = 0 ; j < n - i; j++)

y[j][i] = y[j + 1 ][i - 1 ] - y[j][i - 1 ];

}

for ( int i = 0 ; i < n; i++) {

System.out.print(x[i]+ "\t" );

for ( int j = 0 ; j < n - i; j++)

System.out.print(y[i][j]+ "\t" );

System.out.println();

}

double value = 52 ;

double sum = y[ 0 ][ 0 ];

double u = (value - x[ 0 ]) / (x[ 1 ] - x[ 0 ]);

for ( int i = 1 ; i < n; i++) {

sum = sum + (u_cal(u, i) * y[ 0 ][i]) /

fact(i);

}

System.out.println( "\n Value at " +value+ " is " +String.format( "%.6g%n" ,sum));

}

}

Python3

def u_cal(u, n):

temp = u;

for i in range ( 1 , n):

temp = temp * (u - i);

return temp;

def fact(n):

f = 1 ;

for i in range ( 2 , n + 1 ):

f * = i;

return f;

n = 4 ;

x = [ 45 , 50 , 55 , 60 ];

y = [[ 0 for i in range (n)]

for j in range (n)];

y[ 0 ][ 0 ] = 0.7071 ;

y[ 1 ][ 0 ] = 0.7660 ;

y[ 2 ][ 0 ] = 0.8192 ;

y[ 3 ][ 0 ] = 0.8660 ;

for i in range ( 1 , n):

for j in range (n - i):

y[j][i] = y[j + 1 ][i - 1 ] - y[j][i - 1 ];

for i in range (n):

print (x[i], end = "\t" );

for j in range (n - i):

print (y[i][j], end = "\t" );

print ("");

value = 52 ;

sum = y[ 0 ][ 0 ];

u = (value - x[ 0 ]) / (x[ 1 ] - x[ 0 ]);

for i in range ( 1 ,n):

sum = sum + (u_cal(u, i) * y[ 0 ][i]) / fact(i);

print ( "\nValue at" , value,

"is" , round ( sum , 6 ));

C#

using System;

class GFG

{

static double u_cal( double u, int n)

{

double temp = u;

for ( int i = 1; i < n; i++)

temp = temp * (u - i);

return temp;

}

static int fact( int n)

{

int f = 1;

for ( int i = 2; i <= n; i++)

f *= i;

return f;

}

public static void Main()

{

int n = 4;

double [] x = { 45, 50, 55, 60 };

double [,] y= new double [n,n];

y[0,0] = 0.7071;

y[1,0] = 0.7660;

y[2,0] = 0.8192;

y[3,0] = 0.8660;

for ( int i = 1; i < n; i++) {

for ( int j = 0; j < n - i; j++)

y[j,i] = y[j + 1,i - 1] - y[j,i - 1];

}

for ( int i = 0; i < n; i++) {

Console.Write(x[i]+ "\t" );

for ( int j = 0; j < n - i; j++)

Console.Write(y[i,j]+ "\t" );

Console.WriteLine();

}

double value = 52;

double sum = y[0,0];

double u = (value - x[0]) / (x[1] - x[0]);

for ( int i = 1; i < n; i++) {

sum = sum + (u_cal(u, i) * y[0,i]) /

fact(i);

}

Console.WriteLine( "\n Value at " +value+ " is " +Math.Round(sum,6));

}

}

PHP

<?php

function u_cal( $u , $n )

{

$temp = $u ;

for ( $i = 1; $i < $n ; $i ++)

$temp = $temp * ( $u - $i );

return $temp ;

}

function fact( $n )

{

$f = 1;

for ( $i = 2; $i <= $n ; $i ++)

$f *= $i ;

return $f ;

}

$n = 4;

$x = array ( 45, 50, 55, 60 );

$y = array_fill (0, $n ,

array_fill (0, $n , 0));

$y [0][0] = 0.7071;

$y [1][0] = 0.7660;

$y [2][0] = 0.8192;

$y [3][0] = 0.8660;

for ( $i = 1; $i < $n ; $i ++)

{

for ( $j = 0; $j < $n - $i ; $j ++)

$y [ $j ][ $i ] = $y [ $j + 1][ $i - 1] -

$y [ $j ][ $i - 1];

}

for ( $i = 0; $i < $n ; $i ++)

{

print ( $x [ $i ] . "\t" );

for ( $j = 0; $j < $n - $i ; $j ++)

print ( $y [ $i ][ $j ] . "\t" );

print ( "\n" );

}

$value = 52;

$sum = $y [0][0];

$u = ( $value - $x [0]) / ( $x [1] - $x [0]);

for ( $i = 1; $i < $n ; $i ++)

{

$sum = $sum + (u_cal( $u , $i ) * $y [0][ $i ]) /

fact( $i );

}

print ( "\nValue at " . $value .

" is " . round ( $sum , 6));

Javascript

<script>

function u_cal(u , n)

{

var temp = u;

for ( var i = 1; i < n; i++)

temp = temp * (u - i);

return temp;

}

function fact(n)

{

var f = 1;

for ( var i = 2; i <= n; i++)

f *= i;

return f;

}

var n = 4;

var x = [ 45, 50, 55, 60 ];

var y=Array(n).fill(0.0).map(x => Array(n).fill(0.0));

y[0][0] = 0.7071;

y[1][0] = 0.7660;

y[2][0] = 0.8192;

y[3][0] = 0.8660;

for ( var i = 1; i < n; i++) {

for ( var j = 0; j < n - i; j++)

y[j][i] = y[j + 1][i - 1] - y[j][i - 1];

}

for ( var i = 0; i < n; i++) {

document.write(x[i].toFixed(6)+ "    " );

for ( var j = 0; j < n - i; j++)

document.write(y[i][j].toFixed(6)+ "    " );

document.write( '<br>' );

}

var value = 52;

var sum = y[0][0];

var u = (value - x[0]) / (x[1] - x[0]);

for ( var i = 1; i < n; i++) {

sum = sum + (u_cal(u, i) * y[0][i]) /

fact(i);

}

document.write( "\n Value at " +value.toFixed(6)+ " is " +sum.toFixed(6));

</script>

Output:

          45    0.7071    0.0589    -0.00569999    -0.000699997       50    0.766    0.0532    -0.00639999       55    0.8192    0.0468       60    0.866      Value at 52 is 0.788003

Backward Differences: The differences y1 – y0, y2 – y1, ……, yn – yn–1 when denoted by dy1, dy2, ……, dyn, respectively, are called first backward difference. Thus, the first backward differences are :
\nabla Y_{r}=Y_{r}-Y_{r-1}

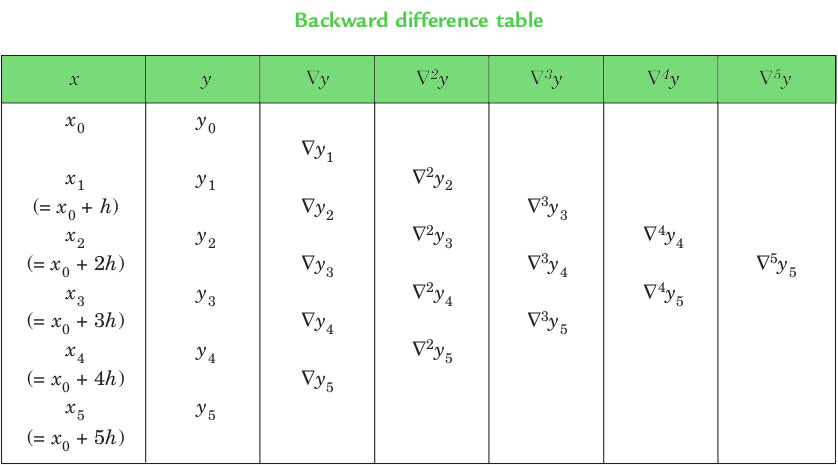
NEWTON'S GREGORY BACKWARD INTERPOLATION FORMULA :
f(a+nh+uh)=f(a+nh)+u\nabla f(a+nh)+\frac{u\left ( u+1 \right )}{2!}\nabla ^{2}f(a+nh)+...+\frac{u\left ( u+1 \right )...\left ( u+\overline{n-1} \right )}{n!}\nabla ^{n}f(a+nh)
This formula is useful when the value of f(x) is required near the end of the table. h is called the interval of difference and u = ( x – an ) / h, Here an is last term.

Example :

Input : Population in 1925

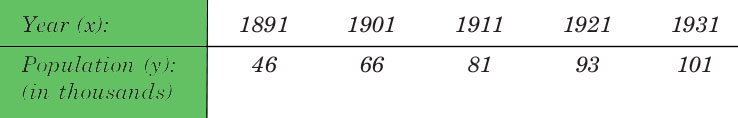
Output :

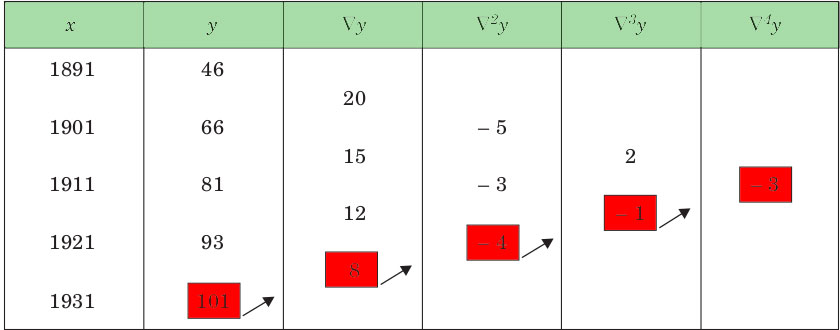
          Value in 1925 is 96.8368

Below is the implementation of the Newton backward interpolation method.

C++

#include <bits/stdc++.h>

using namespace std;

float u_cal( float u, int n)

{

float temp = u;

for ( int i = 1; i < n; i++)

temp = temp * (u + i);

return temp;

}

int fact( int n)

{

int f = 1;

for ( int i = 2; i <= n; i++)

f *= i;

return f;

}

int main()

{

int n = 5;

float x[] = { 1891, 1901, 1911,

1921, 1931 };

float y[n][n];

y[0][0] = 46;

y[1][0] = 66;

y[2][0] = 81;

y[3][0] = 93;

y[4][0] = 101;

for ( int i = 1; i < n; i++) {

for ( int j = n - 1; j >= i; j--)

y[j][i] = y[j][i - 1] - y[j - 1][i - 1];

}

for ( int i = 0; i < n; i++) {

for ( int j = 0; j <= i; j++)

cout << setw(4) << y[i][j]

<< "\t" ;

cout << endl;

}

float value = 1925;

float sum = y[n - 1][0];

float u = (value - x[n - 1]) / (x[1] - x[0]);

for ( int i = 1; i < n; i++) {

sum = sum + (u_cal(u, i) * y[n - 1][i]) /

fact(i);

}

cout << "\n Value at " << value << " is "

<< sum << endl;

return 0;

}

Java

class GFG

{

static double u_cal( double u, int n)

{

double temp = u;

for ( int i = 1 ; i < n; i++)

temp = temp * (u + i);

return temp;

}

static int fact( int n)

{

int f = 1 ;

for ( int i = 2 ; i <= n; i++)

f *= i;

return f;

}

public static void main(String[] args)

{

int n = 5 ;

double x[] = { 1891 , 1901 , 1911 ,

1921 , 1931 };

double [][] y = new double [n][n];

y[ 0 ][ 0 ] = 46 ;

y[ 1 ][ 0 ] = 66 ;

y[ 2 ][ 0 ] = 81 ;

y[ 3 ][ 0 ] = 93 ;

y[ 4 ][ 0 ] = 101 ;

for ( int i = 1 ; i < n; i++)

{

for ( int j = n - 1 ; j >= i; j--)

y[j][i] = y[j][i - 1 ] - y[j - 1 ][i - 1 ];

}

for ( int i = 0 ; i < n; i++)

{

for ( int j = 0 ; j <= i; j++)

System.out.print(y[i][j] + "\t" );

System.out.println( "" );;

}

double value = 1925 ;

double sum = y[n - 1 ][ 0 ];

double u = (value - x[n - 1 ]) / (x[ 1 ] - x[ 0 ]);

for ( int i = 1 ; i < n; i++)

{

sum = sum + (u_cal(u, i) * y[n - 1 ][i]) /

fact(i);

}

System.out.println( "\n Value at " + value +

" is " + String.format( "%.6g%n" ,sum));

}

}

Python3

def u_cal(u, n):

temp = u

for i in range (n):

temp = temp * (u + i)

return temp

def fact(n):

f = 1

for i in range ( 2 , n + 1 ):

f * = i

return f

n = 5

x = [ 1891 , 1901 , 1911 , 1921 , 1931 ]

y = [[ 0.0 for _ in range (n)] for __ in range (n)]

y[ 0 ][ 0 ] = 46

y[ 1 ][ 0 ] = 66

y[ 2 ][ 0 ] = 81

y[ 3 ][ 0 ] = 93

y[ 4 ][ 0 ] = 101

for i in range ( 1 , n):

for j in range (n - 1 , i - 1 , - 1 ):

y[j][i] = y[j][i - 1 ] - y[j - 1 ][i - 1 ]

for i in range (n):

for j in range (i + 1 ):

print (y[i][j], end = "\t" )

print ()

value = 1925

sum = y[n - 1 ][ 0 ]

u = (value - x[n - 1 ]) / (x[ 1 ] - x[ 0 ])

for i in range ( 1 , n):

sum = sum + (u_cal(u, i) * y[n - 1 ][i]) / fact(i)

print ( "\n Value at" , value, "is" , sum )

C#

using System;

class GFG

{

static double u_cal( double u, int n)

{

double temp = u;

for ( int i = 1; i < n; i++)

temp = temp * (u + i);

return temp;

}

static int fact( int n)

{

int f = 1;

for ( int i = 2; i <= n; i++)

f *= i;

return f;

}

static void Main()

{

int n = 5;

double [] x = { 1891, 1901, 1911,

1921, 1931 };

double [,] y = new double [n,n];

y[0,0] = 46;

y[1,0] = 66;

y[2,0] = 81;

y[3,0] = 93;

y[4,0] = 101;

for ( int i = 1; i < n; i++)

{

for ( int j = n - 1; j >= i; j--)

y[j,i] = y[j,i - 1] - y[j - 1,i - 1];

}

for ( int i = 0; i < n; i++)

{

for ( int j = 0; j <= i; j++)

Console.Write(y[i,j]+ "\t" );

Console.WriteLine( "" );;

}

double value = 1925;

double sum = y[n - 1,0];

double u = (value - x[n - 1]) / (x[1] - x[0]);

for ( int i = 1; i < n; i++)

{

sum = sum + (u_cal(u, i) * y[n - 1,i]) /

fact(i);

}

Console.WriteLine( "\n Value at " +value+ " is " +Math.Round(sum,4));

}

}

PHP

<?php

function u_cal( $u , $n )

{

$temp = $u ;

for ( $i = 1; $i < $n ; $i ++)

$temp = $temp * ( $u + $i );

return $temp ;

}

function fact( $n )

{

$f = 1;

for ( $i = 2; $i <= $n ; $i ++)

$f *= $i ;

return $f ;

}

$n = 5;

$x = array (1891, 1901, 1911,

1921, 1931);

$y = array_fill (0, $n , array_fill (0, $n , 0));

$y [0][0] = 46;

$y [1][0] = 66;

$y [2][0] = 81;

$y [3][0] = 93;

$y [4][0] = 101;

for ( $i = 1; $i < $n ; $i ++)

{

for ( $j = $n - 1; $j >= $i ; $j --)

$y [ $j ][ $i ] = $y [ $j ][ $i - 1] -

$y [ $j - 1][ $i - 1];

}

for ( $i = 0; $i < $n ; $i ++)

{

for ( $j = 0; $j <= $i ; $j ++)

print ( $y [ $i ][ $j ] . "\t" );

print ( "\n" );

}

$value = 1925;

$sum = $y [ $n - 1][0];

$u = ( $value - $x [ $n - 1]) / ( $x [1] - $x [0]);

for ( $i = 1; $i < $n ; $i ++)

{

$sum = $sum + (u_cal( $u , $i ) *

$y [ $n - 1][ $i ]) / fact( $i );

}

print ( "\n Value at " . $value .

" is " . round ( $sum , 4));

?>

Javascript

<script>

function u_cal(u , n)

{

var temp = u;

for ( var i = 1; i < n; i++)

temp = temp * (u + i);

return temp;

}

function fact(n)

{

var f = 1;

for ( var i = 2; i <= n; i++)

f *= i;

return f;

}

var n = 5;

var x = [ 1891, 1901, 1911,

1921, 1931 ];

var y = Array(n).fill(0.0).map(x => Array(n).fill(0.0));

y[0][0] = 46;

y[1][0] = 66;

y[2][0] = 81;

y[3][0] = 93;

y[4][0] = 101;

for ( var i = 1; i < n; i++)

{

for ( var j = n - 1; j >= i; j--)

y[j][i] = y[j][i - 1] - y[j - 1][i - 1];

}

for ( var i = 0; i < n; i++)

{

for ( var j = 0; j <= i; j++)

document.write(y[i][j] + "\t" );

document.write( '<br>' );;

}

var value = 1925;

var sum = y[n - 1][0];

var u = (value - x[n - 1]) / (x[1] - x[0]);

for ( var i = 1; i < n; i++)

{

sum = sum + (u_cal(u, i) * y[n - 1][i]) /

fact(i);

}

document.write( "\n Value at " + value +

" is " +sum);

</script>

Output:

          46       66      20       81      15      -5       93      12      -3       2      101       8      -4      -1      -3       Value at 1925 is 96.8368

Time Complexity : O(N*N) ,N is the number of rows.

Space Complexity : O(N*N) ,for storing elements in difference table.

This article is contributed by Shubham Rana. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.


hodgescopiche.blogspot.com

Source: https://www.geeksforgeeks.org/newton-forward-backward-interpolation/

0 Response to "Forward Difference Error Function Only Continuous"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel